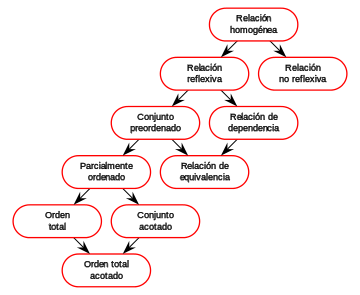
En teoría de conjuntos, la noción de relación de equivalencia sobre un conjunto, permite establecer una relación entre los elementos del conjunto que comparten cierta característica o propiedad. Esto permite reagrupar dichos elementos por clase de equivalencia, es decir, «paquetes» de elementos similares. A su vez, esto posibilita la construcción de nuevos conjuntos «asimilando» todos los elementos de una misma clase a un solo y único elemento, lo que define la noción de conjunto cociente.




 un
un  una
una  .
.
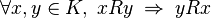
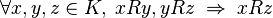
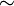 sobre un conjunto
sobre un conjunto 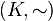 .
.